I'm unsatisfied with easing functions

July 15, 2025

You've probably encountered easing functions before. If you're a creative coder, you've likely heard of them or used them. If you're a user, you've certainly interacted with them. They're everywhere, and they give a little more life to computer generated animations.

Taking it easy

For the uninitiated: let's say you've got a circle that you want to move from left to right over the course of a second. We can conceptualize this by converting the time into progress: a value between 0 and 1, representing how far through the animation we are. 0 represents the start of the animation, and 1 represents the end. Then, we can convert that progress to a position to draw the circle at.

function setup() {
  createCanvas(200, 200);
}

function draw() {
  background('white');
  fill('red');

  let progress = map(millis() % 3000, 1000, 2000, 0, 1, true);
  let x = lerp(50, 150, progress);
  circle(x, height/2, 20);
}

This looks pretty mechanical. Animators may be able to articulate exactly why. A book written by Disney animators outlines the 12 principles of animation, and these have become an essential part of an animation education. They're a set of things to think about as you animate to help bring characters believably to life (or, as rules to break at opportune moments for shock or comedy.) One of the principles is slow in, slow out. Basically: an object starting from rest takes some time to accelerate, and an object coming to a stop has to take time to decelerate. It's a high-level consequence of laws of physics, really. And our initial code violates it by suddenly jolting our circle to a constant speed, before suddenly stopping it again.

So what do you do about it? The answer for many is to slap an easing function on it! An easing function takes in a linear progress value, and returns a new progress value, but converted to nonlinear motion. Say you've copy-and-pasted in a stock easing function with an ease in and ease out. Now, your code could look like this:

function setup() {
  createCanvas(200, 200);
}

function draw() {
  background('white');
  fill('red');

  let progress = map(millis() % 3000, 1000, 2000, 0, 1, true);
  progress = easeInOutCubic(progress);
  let x = lerp(50, 150, progress);
  circle(x, height/2, 20);
}

function easeInOutCubic(t) {
  return t < 0.5
    ? (t * 2) ** 3 * 0.5
    : (1 - Math.abs(((t * 2) - 2) ** 3)) * 0.5 + 0.5;
}

Now, it looks a little more natural!

You've got some other options, too. If you want to add overshoot, related to another principle of animation, follow through. You could use easeOutElastic:

function setup() {
  createCanvas(200, 200);
}

function draw() {
  background('white');
  fill('red');

  let progress = map(millis() % 3000, 1000, 2000, 0, 1, true);
  progress = easeOutElastic(progress);
  let x = lerp(50, 150, progress);
  circle(x, height/2, 20);
}

function easeOutElastic(t, magnitude = 0.7) {
  const p = 1 - magnitude;
  const scaledTime = t * 2;

  if ( t === 0 || t === 1 ) {
    return t;
  }

  const s = p / (2 * Math.PI) * Math.asin(1);
  return 2 ** (-10 * scaledTime)
    * Math.sin((scaledTime - s)
    * (2 * Math.PI) / p) + 1;
}

If you want one that also adds some anticipation, you could maybe use easeInOutBack:

function setup() {
  createCanvas(200, 200);
}

function draw() {
  background('white');
  fill('red');

  let progress = map(millis() % 3000, 1000, 2000, 0, 1, true);
  progress = easeInOutBack(progress);
  let x = lerp(50, 150, progress);
  circle(x, height/2, 20);
}

function easeInOutBack(t, magnitude = 0.7) {
  const c1 = 1.70158
  const c2 = c1 * 1.525
  return t < 0.5
    ? (pow(2 * t, 2) * ((c2 + 1) * 2 * t - c2)) / 2
    : (pow(2 * t - 2, 2) * ((c2 + 1) * (t * 2 - 2) + c2) + 2) / 2;
}

All of these look way less mechanical than the original, and all set a different tone. Nice!

Easing is not so easy

If you're a programmer, you may even be able to clock specific easing functions by looking at them. That's maybe where the problems begin for me. There's just too few of them!

There's really nothing wrong with them. But you just end up picking one out of a couple stock choices, and that means you end up repeating them. In traditional animation, the principles are just guidelines; you still end up creating new unique motion each time based on what acting the scene calls for. Easing functions in code don't quite give you the flexibility to do that.

Some other alternatives have been proposed, though.

Apple's kinematic easing functions

A paper from Apple describe a parameterizable easing function. It's a single function, but it lets you tweak some of its properties, including whether or not it includes anticipation, and if there's overshoot, how many oscillations it has.

It's a great idea, but there is some friction that I run into when using it.

The workflow is, I set up a base linear motion with approximate timing. I then wrap the linear progress in this kinematic easing function, and tweak its parameters. When I adjust properties such as the number of oscillations, it also affects other properties I would want to hold constant, such as the how far it overshoots. Adjusting the acceleration brings it back, but then affects the size of the anticipation too. I end up having to twiddle with multiple parameters at once to narrow down on the intended result.
Changing the number of oscillations also changes the frequency of the system: more oscillations makes the animation play faster unless you manually adjust the duration of the animation too. This gets at a fundamental issue with regular easing functions, too: you have to specify the timing and make it look good. What looks decent for cubic ease-in-ease-out may look unnaturally fast for elastic ease out.
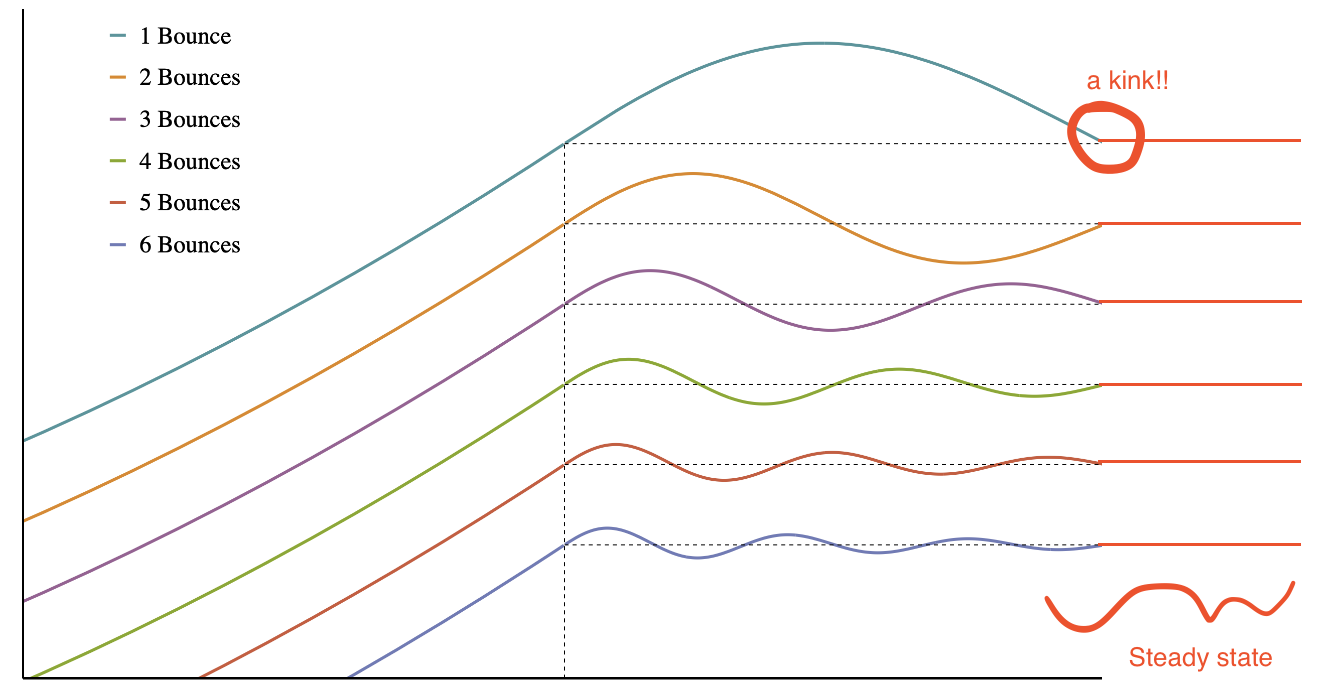
Try setting damping to 0 and adding a single oscillation. The overshoot tends to feel like it comes to a sudden stop. If you look at a graph of progress over time, it looks like there is a slight kink at the end of the curve as it hits a steady state value of 1 at the end. This can be addressed with damping, but adjusting this also adjusts the size of the overshoot, meaning I have to mess with the acceleration, which causes more updates to be required.

A diagram from the paper showing oscillations, damping-free. If you extend the diagram out to the right at the steady state value, you can see where a visual jump will occur due to a kink in the motion curve.

Convolution filter

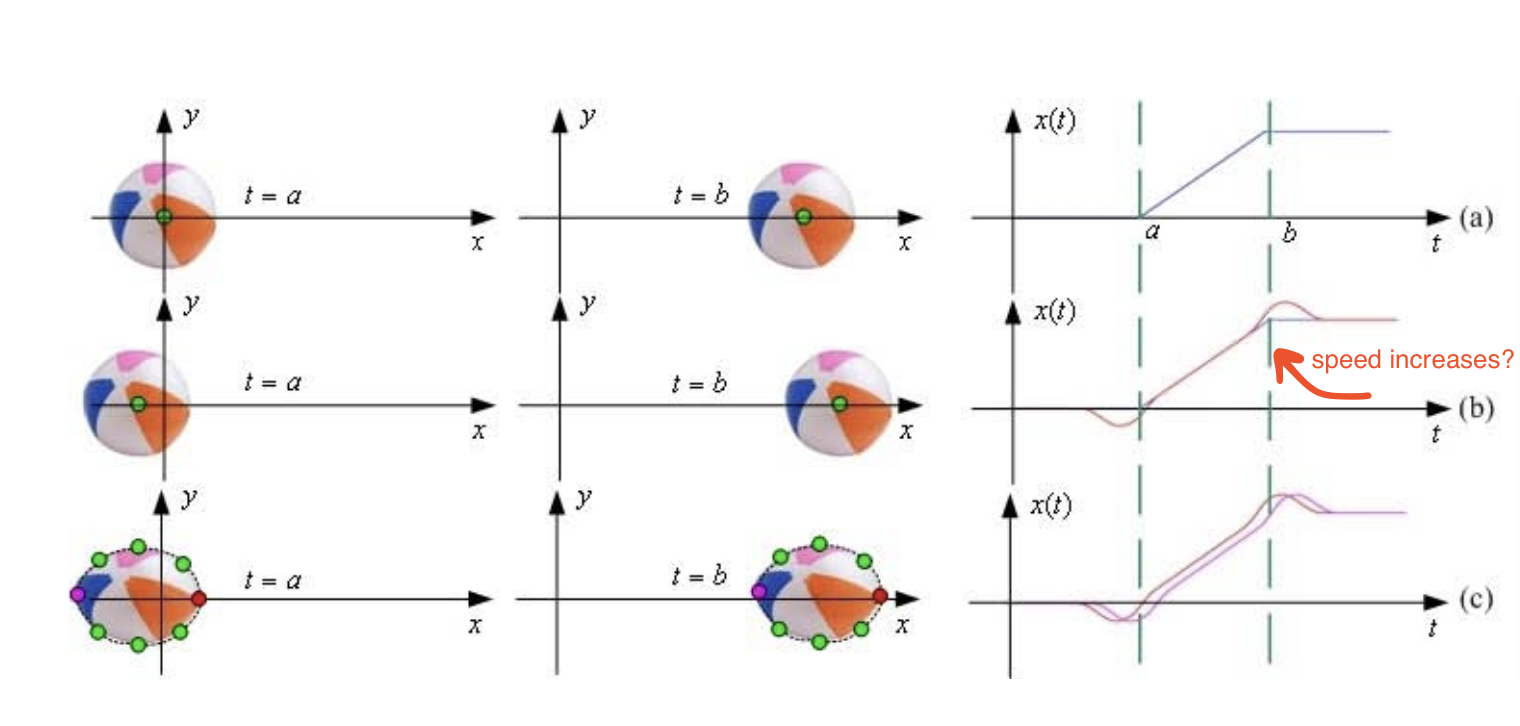
Another paper describes an approach that breaks from easing functions: use the convolution of the original motion with a Laplacian-of-Gaussian filter that adds an anticipation and overshoot. This is also a cool idea! It works on any stream of input, not just a single 0-1 transition progress. Here's what a simple linear motion looks like when filtered:

It definitely has anticipation and overshoot, but something looks... off.

In the paper, they show a filtered version of simple linear motion curve, like what we've got above. The main issue I see is that the motion speeds up into the overshoot:

A diagram from the paper showing filtered linear motion. The slope of the curve changes at the anticipation and overshoot, though.

This misunderstands something about overshoot, I think. Why would the object speed up there? Overshoot generally occurs because an object didn't start slowing down early enough, not because it sped up to go further. So I think this approach isn't quite practical; overshoot speed needs to be consistent with the speed going into the overshoot.

Feedback control

Another non-easing-function approach that's decades old is to use a feedback control system to make an object follow a target. A feedback controller, as the name suggests, controls some variables in a system based on observations of the output of the system. In our case, a controller can apply something akin to force on an object by observing its position and velocity.

Here's a demo of proportional + derivative (PD) control over motion. (Often, there will also be an integral term and it will be called a PID controller; I've omitted that for simplicity and to mimic a mass + spring + damper system.) Try adjusting the frequency and damping and frequency and then tapping on canvas to change the target:

By setting the damping above the midpoint value, you get a smooth ease out as it reaches the target value. By setting it lower, you get an overshoot and oscillation. The frequency slider affects how fast the movement and oscillations happen.

This setup is nice in that you don't control the timing at all: the timing is just a result of the parameters of the controller. If you make it follow something farther away, it will naturally take longer and overshoot more. I still have some issues with using it for programmatic animation though.

It's still a little finnicky to control. Both the damping and frequency affect how fast it reaches a target, leading to twiddling. Not as much as before though!
More fundamentally, this type of system does not try to do any anticipation. You could manually move your target back first before going forward. That could be something?
This also generally implemented with a simulation of sorts. One really nice property of regular easing functions is that you can seek anywhere in time and know exactly where everything should be. With a simulation, you must start from time 0 and step forwards to compute where everything should be. For inputs to a controller that are known ahead of time (e.g. if your target is always a linear ramp from 0-1), then there are closed-form formulas for the response, so a simulation would no longer be necessary. So a potentially promising approach could be to see if you can make an easing function out of the response to a (maybe parameterized?) fixed input, or possibly splicing two responses together to handle anticipation + overshoot. Thanks to Greg Stanton for pointing out the opportunity here!

Future easing?

I don't have any alternative to propose just yet. And clearly the existing options have been working well enough for people! One can certainly be productive with them, and one can pick the right tool for the job.

That said, I think it's possible to do something better. All the approaches I've mentioned have their merits, but also have drawbacks that make them not quite the full system I want. Maybe each could be modified in some way to get some more desirable properties? It could just take some time and some tinkering to explore more.

I probably will get around to this eventually since I keep ranting to my sister about how I think this could be improved. But it hasn't been so pressing that I've made the time to really look into it. I too find the current solutions good enough for most things. So I figured, maybe I can start by just writing up my rant, and maybe someone else will read this and find a Research Project in here and will make the time before me. If that sounds like you, feel free to reach out to me, I'm happy to consult and provide some direction!

And if not, maybe in a year or so I'll get around to tinkering more and I'll post a follow-up with some new system.