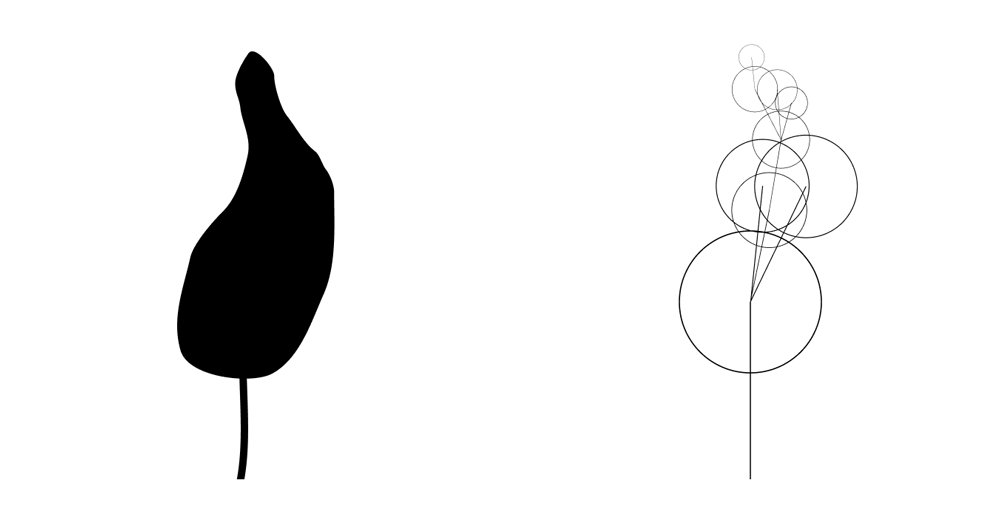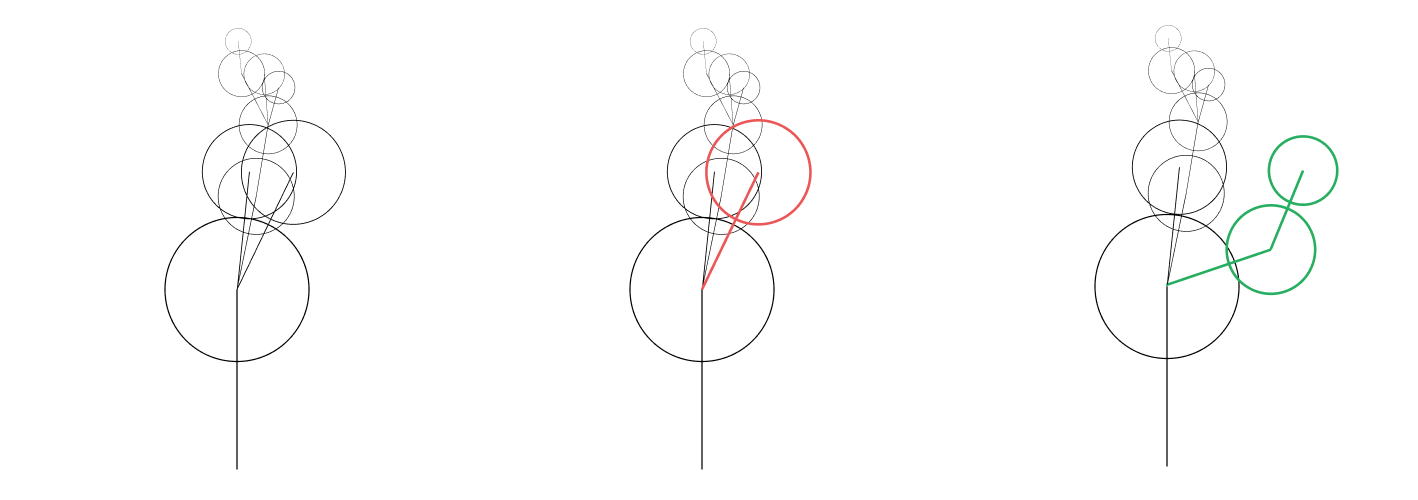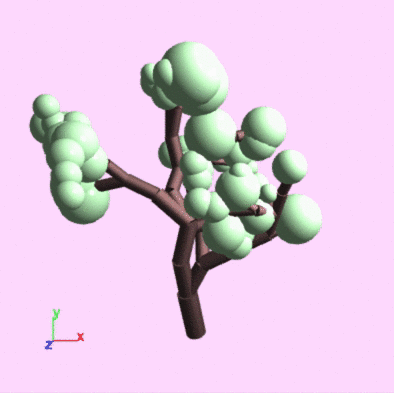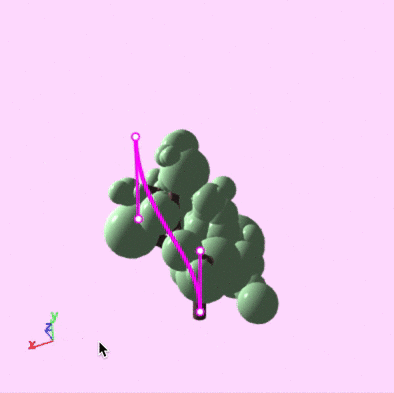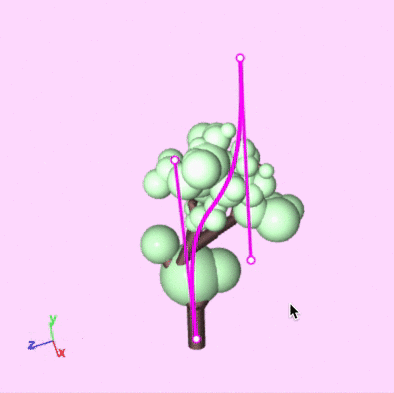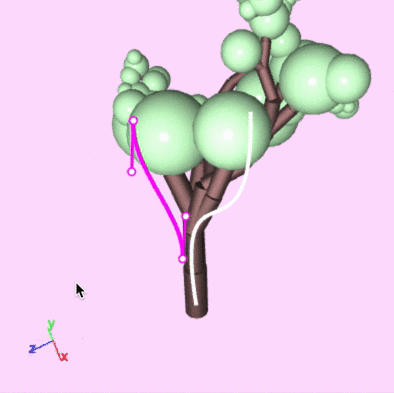Improving the procedural modelling workflow
There are a lot of things in art that are hard, but are especially hard in 3D.
Say you wanted to make a forest landscape. If this were a painting, you probably wouldn't paint every leaf on every tree. Firstly, you don't have to worry about the ones you can't see. But even for the ones you can see, you're able to get away with using less detail in areas that aren't the focus. The patterns can be abstracted into dabs of paint that give the impression of leaves without the effort of clearly defining each one.
3D doesn't afford this luxury. For better or for worse, everything in 3D graphics as we know it must be attached to some well-defined form. There's no way to dab a brush here and there just yet. Less detail could be used off in the distance, but in many cases, 3D is being used specifically so that a world can be inhabited, walked around, and explored, so there may not be a region that's "in the distance" all the time.
You can try to save effort by modelling a tree and copy-and-pasting it around. Of course, the difficulty with this is that the regularity will look unnatural. You can rotate and distort them as you go to add some variation, and that may help, but it can only go so far. To get rid of that unwanted regularity, you'd want to apply the same process to components of each pasted tree, not just the whole thing, so that the overall model looks different. While this may be faster than modelling each tree from scratch, this still ends up being a lot of manual effort.
It gets to a point where it becomes easier to describe the procedure with which models are created than to create the models by hand. This is what procedural modelling is: the creation of a program of sorts that then creates models. I've spent a fair amount of time recently trying to make this process better, so I'm going to explain some background and the techniques I used.
Generating from grammars
Grammars are a convenient way of describing the sorts of patterns we want in our models. The name comes from how we describe the patterns in the structure of language. English, for example, has a grammar. You may have seen a sentence broken up into a structure like this:
| The | handsome | author | disseminated | knowledge | from | his | expansive | brain. |
|---|---|---|---|---|---|---|---|---|
| ARTICLE | ADJ | NOUN | VERB | NOUN | PREP | ADJ | ADJ | NOUN |
| NOUN PHRASE | NOUN PHRASE | |||||||
| NOUN PHRASE | ||||||||
| VERB PHRASE | ||||||||
| CLAUSE | ||||||||
| SENTENCE | ||||||||
Let's simplify things and ignore a bunch of parts of the English language to make a simple grammar, where everything is either a noun, a verb, or the joiner word "and."
| I | say | words. |
|---|---|---|
| NOUN | VERB | NOUN |
| VERB PHRASE | ||
| CLAUSE | ||
| SENTENCE | ||
If you read the sentence breakdown from the bottom up, you can see how one component of the sentence can be composed of multiple other components, eventually leading to concrete words. We'll call the concrete words terminals and we'll call the components rules. We can describe how it all works for our simplified version of English by showing the different ways you can break down each rule, starting from the broadest.
As a convention, things in ALL CAPS will be rules and things in lowercase will be terminals. A | means "or," with brackets to help specify how alternatives are grouped. The symbol ε refers to nothing, so (x | ε) effectively means x is optional.
| SENTENCE | CLAUSE (COMPOUND | ε) |
|---|---|
| COMPOUND | and CLAUSE (COMPOUND | ε) |
| CLAUSE | NOUN VERB_PHRASE |
| VERB_PHRASE | VERB (NOUN | ε) |
| NOUN | abacus | babboon | cantaloupe | ... |
| VERB | arrive | bamboozle | capitulate | ... |
You can see how these definitions can be used to produce the sentence breakdown from earlier, starting from a sentence, breaking that down into a clause, and then a noun and verb phrase. An existing sentence can be analyzed by starting from the words in the sentence, grouping terminals into rules, and then grouping the rules into more rules, until no more grouping is possible.
You can also go the other way to generate sentences. Start from a rule, pick some arbitrary breakdown of that rule into more rules, and eventually pick arbitrary terminals from the available options:
| SENTENCE | ||||||
| CLAUSE | COMPOUND | |||||
| NOUN | VERB PHRASE | and | CLAUSE | |||
|---|---|---|---|---|---|---|
| Ants | VERB | NOUN | NOUN | VERB PHRASE | ||
| cover | surfaces | I | VERB | NOUN | ||
| raise | concerns. | |||||
In a way, it's like Mad Libs, but where the sentence structure is also picked at random in addition to the words.
Grammars for constructing shapes
Just like words, this can be done with shapes. We'll need a new vocabulary, though. Instead of generating an English sentence, we'll generate a set of instructions telling the computer how to draw something.
We'll start with a simple system, just like we did with English. We'll work in 2D, but all of these concepts can be extended directly to 3D. Instead of terminals being nouns, verbs, and "and," our terminals will be one of the following:
- lineTo(x, y): Draw a line from the current point to the offset x, y
- circle(radius): Draw a circle with a given radius
- translate(x, y): Move the paper being drawn on by an offset
- rotate(angle): Rotate the paper being drawn on
- scale(factor): Make the paper being drawn on bigger or smaller (OK, this is stretching the "paper" metaphor, both literally and figuratively)
Before making a grammar with these, let's use these tools to draw a tree. We can start with a branch and a circle at first. In the examples below, I'm working in a 100-by-100 canvas where the point (0, 0) is right in the middle. I've drawn a box showing the size and orientation of the paper after each operation, with crosshairs on (0, 0), for reference.
| translate(0, 50) | lineTo(0, -50) | translate(0 -50) | circle(20) |
|---|
Let's say we want to copy-and-paste this unit around at different scales. To not have to change the numbers in the command, we can make use of the scale() command in between pastes of the lineTo() and circle() commands.
| translate(0, 50) | lineTo(0, -50) | translate(0, -50) | circle(20) |
|---|---|---|---|
| scale(0.5) | lineTo(0, -50) | translate(0, -50) | circle(20) |
We could conceivably keep scaling and pasting to make ever larger trees until we decide to stop. Although it's a simple pattern, it's still a pattern, so we can represent this procedure in a grammar. We start off by placing the pen at the bottom of the frame, drawing a branch like before, and then optionally scaling and adding another branch ad infinitum.
| TREE | translate(0, 50) BRANCH |
|---|---|
| BRANCH | lineTo(0, -50) translate(0, -50) circle(20) (SUB_BRANCH | ε) |
| SUB_BRANCH | scale(0.5) BRANCH |
If we randomly generate from this grammar, giving each choice an equal probability when picking a way to break down a rule, we'll basically just end up with trees of varying heights depending on how many times SUB_BRANCH is picked over ε when expanding the BRANCH rule.
| translate(0, 50) | BRANCH | scale(0.5) | BRANCH |
|---|---|---|---|
| scale(0.5) | BRANCH | scale(0.5) | BRANCH |
What should we do if we want to add more than one sub branch off of an initial branch? It looks like we would have to rewind the translations we applied by applying the inverse (e.g. translate(0, 50) to undo translate(0, -50).) That would work, but it would be tedious. Instead, we can add some new commands to our vocabulary. Here are two more drawing commands to allow us to backtrack to old orientations of the paper:
- [: Remember the position, rotation, and scale of the paper by adding it to a stack of saved orientations
- ]: Take the last saved paper orientation from the stack and restore it
Now, let's make a tree that branches into two each time. Instead of scaling and adding a branch, we'll scale, save the position, rotate to the left, add a branch, restore the position, rotate to the right, and add another branch.
| TREE | translate(0, 50) BRANCH |
|---|---|
| BRANCH | lineTo(0, -50) translate(0, -50) circle(30) (SUB_BRANCHES | ε) |
| SUB_BRANCHES | scale(0.5) [ rotate(-30) BRANCH ] [ rotate(20) BRANCH ] |
This is what happens when you generate trees using the stack of remembered orientations:
| translate(0, 50) | BRANCH | scale(0.5) | |||
|---|---|---|---|---|---|
| [ | rotate(-30) | BRANCH | scale(0.5) | ||
| [ | rotate(-30) | BRANCH | ] | ||
| [ | rotate(30) | BRANCH | ] | ] | |
| [ | rotate(30) | BRANCH | scale(0.5) | ||
| [ | rotate(-30) | BRANCH | ] | ||
| [ | rotate(30) | BRANCH | ] | ] |
This lets us express a lot of ideas, but it suffers from the problem mentioned earlier when discussing copy-and-pasting: it looks too regular. We can introduce random variation into our grammar by replacing concrete numbers with random(a, b), which, when interpreted by the drawing program, will generate a random number between a and b inclusive.
Here's our grammar again, with random variation added in the highlighted rule definition:
| TREE | translate(0, 50) BRANCH |
|---|---|
| BRANCH | lineTo(0, -50) translate(0, -50) circle(30) (SOME_BRANCHES | ε) |
| SOME_BRANCHES | SCALED_BRANCH (SOME_BRANCHES | ε) |
| SCALED_BRANCH | [ scale(random(0.4, 0.8)) rotate(random(-40, 40)) BRANCH ] |
The scale is now a random amount, and so is the rotation. Additionally, instead of generating exactly two sub-branches, it can generate anywhere between 0 and infinity, much in the same way that our first tree grammar could stack branches vertically possibly infinite times. This happens because SOME_BRANCHES makes one branch, and then maybe adds yet another SOME_BRANCHES rule.
Here are some trees that get generated from this grammar:
One thing that might strike you about these examples is that they aren't really all that nice to look at. Some of them are, but others stop growing too early, and others have fairly unnatural branching. How does one deal with that?
Controlling procedural modelling at the grammar level
The problem we're facing is that our grammar can generate the things we want, but it can also generate other technically valid things that are decidedly not what we want.
We could try adjusting our grammar to not be able to generate these undesirable outputs, but that gets hairy pretty quickly. Let's look at sentences again, because the same problem applies. Say we want to prevent run-on sentences like the following:
| The years keep coming | and | they don't stop coming | and | they don't stop coming | and | they don't stop coming | and | they don't stop coming |
|---|---|---|---|---|---|---|---|---|
| CLAUSE | CLAUSE | CLAUSE | CLAUSE | CLAUSE | ||||
| COMPOUND | ||||||||
| COMPOUND | ||||||||
| COMPOUND | ||||||||
| COMPOUND | ||||||||
| SENTENCE | ||||||||
How would you cap the number of chained clauses to, say, four? There's no magic constant in the grammar that you can change from infinity to four. You could maybe flatten out the self-referential nature of the COMPOUND rule, making it instead look something like this:
| SENTENCE | CLAUSE COMPOUND |
|---|---|
| COMPOUND | (and CLAUSE | ε) (and CLAUSE | ε) (and CLAUSE | ε) (and CLAUSE | ε) |
| CLAUSE | NOUN VERB_PHRASE |
| VERB_PHRASE | VERB (NOUN | ε) |
| NOUN | abacus | babboon | cantaloupe | ... |
| VERB | arrive | bamboozle | capitulate | ... |
If you wanted a number larger than four, but still a finite number, you might have to do a lot of copy-and-pasting. You almost start wanting to have a program to help write your program to generate sentences. That seems like overkill, and also might not help with more complicated scenarios. For trees, how would you specify a different set of branching angles for branches nested between 3 and 5 levels deep? You could copy-and-paste rules again and have a separate branch rule for each nesting level. It quickly becomes unmanageable.
But there's a better way!
Controlling procedural modelling using search
Especially when dealing with grammars, it can often be easier to specify whether a result is good or not than to specify how to produce good results. In the motivating example of tree generation, perhaps a silhouette can be quickly freehanded, and we want the computer to produce a detailed tree with leaves that fills the silhouette decently.
We can assign a score to every picture representing how close its silhouette is to the target. It might look something like this, in pseudocode:
function score(image) {
// First, fill all the shapes in the outputted image
// to get its silhouette
let filled = flood_fill_all_gaps(image)
// Count how many pixels in that silhouette are the
// same as the corresponding pixel in the target
let num_same = 0
for (x, y) in filled {
if filled.color_at(x, y) == target.color_at(x, y) {
num_same = num_same + 1
}
}
return num_same
}
Now, rather than trying to describe how to produce good images without accidentally making bad ones, we have a search problem where we are trying to find an image produced by a grammar that maximizes score.
One conceptually simple way to do that would be to generate a lot of samples, calculate the score for each one, and then pick the one with the best score. I'll say right away that this method won't be the best one because grammars produce a really large space of images, so the likelihood that you get a good one from a reasonably sized set of samples is low. Let's take a moment to explore just how low.
Procedural models as probabilistic samples
Let's assume the tree above is the optimal tree for the silhouette I provided for some definition of optimality. What is the probability that this particular tree would be generated from the grammar we made?
When we define a grammar, we are also defining the set of all possible things it can create. It is the set of all the possible strings of instructions you could end up with from all the possible breakdowns of rules that would be allowed by the grammar. Each time a choice is made when deciding how to expand rules into other rules, the end result becomes less and less likely to be generated randomly. There are two kinds of choices that we make:
- Every time a | is used in the grammar to indicate a choice. Say we have (BRANCH | ε) in a rule. We have been assuming so far that there is a 50% chance that this gets expanded to a BRANCH rule and a 50% chance that it is expanded to ε and stops there. After going down either path, the probability for the model that gets generated is cut in half. Although we haven't given a way to specify it, you can imagine having choices without an equal split (for example, 60-40 instead of 50-50.) In those cases, going down the left path would lead to model probabilities being multiplied by 0.6, and going down the right path would lead to model probabilities being multiplied by 0.4.
- Every time random(a, b) is used. If this produces a random value from a continuous distribution, then technically there is a probability of 0 that a specific value is chosen (e.g. 0.5 rather than 0.4999... or 0.500...01.) In practice, as a substitute, we can look at the random number generator's probability density function (pdf) as a measure of how likely a given value is compared to other values. The total area under a pdf curve from negative infinity to infinity is always 1, and is distributed across that domain according to how likely that region is to be generated. If random(0, 1) is uniformly distributed, the pdf of any value between 0 and 1 is 1, indicating that they are equally likely.
Starting with the first case, our grammar requires making one choice for every branch present after the first one. There are eight branches off of the base one in the particular tree shown earlier, so the probability of generating the same structure of that tree is 0.58 = 0.00390625. To look at the second case, if we make a generous approximation and assume random() generates one of ten values within a given range each time, then because each branch makes two of these calls, we introduce a factor of (0.1 × 0.1)8 = 1 × 10-16. Altogether, that's around 3.9 × 10-19. You will need a lot of random samples to generate a tree in this particular configuration. This is all a contrived example, since we never have one exact tree we are hoping to produce, but the point here is that there are many possibilities in the grammar output.
Luckily, there are ways to focus the search.
Markov Chain Monte Carlo sampling
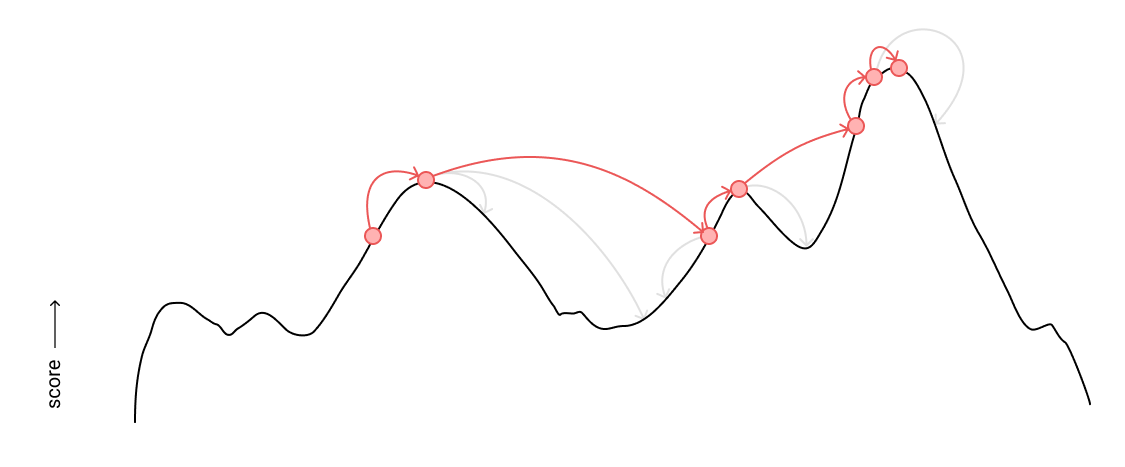
The previous method of simply generating a lot of samples and taking the best ones wastes a lot of valuable information that can be used to refine the search. Markov Chain Monte Carlo (MCMC) sampling is an attempt to make use of the information we get by looking at a number of samples.
In MCMC sampling, we first generate a random image using the grammar, and hold onto that as our reference image. Then, we produce a slightly mutated version of the image. If the mutated version has a better score, we use that as the reference image and mutate this new image in the next iteration instead of the old image. If the mutated image has a lower score, we might still randomly use it as the new reference, with a higher likelihood the closer it is to the score of the existing reference. The idea is that, over enough samples, the reference sample reaches an optimal score. Allowing it the possibility to jump to a lower score allows it to not get stuck at a local maximum when higher score peaks may exist elsewhere, and given enough time, it will probabilistically explore the space and converge on a good value.
Here is the algorithm, written out into steps:
- Initially define reference by generating a shape from the grammar.
- Make a new shape, proposal, by mutating the current reference.
- If likelihood(proposal) * score(proposal) is greater than likelihood(reference) * score(reference), set reference = proposal.
- If proposal had did not have a better score, only set reference = proposal if a random number between 0 and 1 is less than (likelihood(proposal) * score(proposal)) / (likelihood(reference) * score(reference)).
- Return to step 2.
A note on mutations
What does it actually mean to say that we "mutate" the image? There is some precedent set by grammar-based algorithms in other domains.
When writing computer programs, we often also write accompanying tests that use the program and assert that it did the thing we expected them to do. Mutations are useful for determining how good these tests are. An example of a bad test is one that simply runs assert(1 == 1) and nothing else, as this does not depend on the program being tested at all. The basic idea of mutation testing is that if you randomly change a part of the program source code, this probably makes it work incorrectly, and the test suite should catch it. If it doesn't catch it, it probably indicates that the part of the source code that was mutated isn't tested very well.
Since the source code for a program conforms to a grammar just like human language does, one can look at the grammar breakdown for some source code, and then replace a part of it with some other part to generate a mutant to run tests on. Say you have a part of the grammar talking about assignments and arithmetic:
| ... | |
| ASSIGNMENT | IDENTIFIER = EXPRESSION |
|---|---|
| EXPRESSION | (IDENTIFIER | NUMBER) (OPERATOR EXPRESSION | ε) |
| OPERATOR | + | - | * | / |
| ... |
And then you maybe have a line like this in your program:
| something | = | something | + | 1 |
|---|---|---|---|---|
| IDENTIFIER | IDENTIFIER | OPERATOR | NUMBER | |
| EXPRESSION | ||||
| EXPRESSION | ||||
| ASSIGNMENT | ||||
To generate a mutant, we want to replace some subtree of the breakdown above with a different option from the grammar. We can see that there is an EXPRESSION rule which is just a NUMBER with a 1 in it. We could replace it with a different EXPRESSION that is just as valid, such as 1 / 8.
| something | = | something | + | 1 | / | 8 |
|---|---|---|---|---|---|---|
| IDENTIFIER | IDENTIFIER | OPERATOR | NUMBER | OPERATOR | NUMBER | |
| EXPRESSION | ||||||
| EXPRESSION | ||||||
| EXPRESSION | ||||||
| ASSIGNMENT | ||||||
The hope is that some test notices that things stop working the same way after making this mutation, and if it doesn't notice, we should write a test that uses this part of the source code.
For MCMC sampling of our images, we do something similar. An image is actually the product of a decision tree we made as we broke down rules into more rules to generate the drawing instructions. We can make a new image by taking a subtree of the original image's drawing instructions grammar breakdown and replacing it with a different but also valid subtree. When picking a subtree to replace, we want to have the likelihood of a given subtree being replaced to be proportional to the likelihood of that subtree being generated in the first place so that we don't spend a disproportionate amount of time messing around in the little details of the extremities of a shape. We already talked about how likely a whole image is to be generated, and the likelihood of a subtree being generated is pretty much the same. The only difference is that we start looking at choices made at the beginning of a subtree rather than at the very top of the whole breakdown.
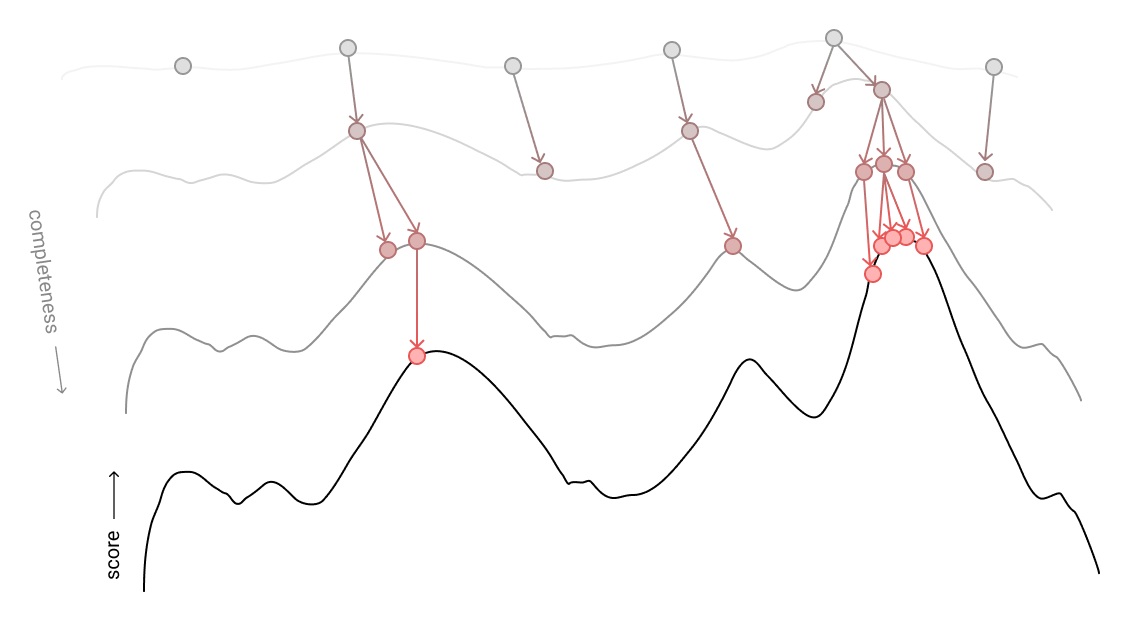
Improving the sampling performance with Sequential Monte Carlo sampling
Unfortunately, MCMC sampling with a silhouette-matching score function is still not fast. In 3D, it can take hours to match a generated model to a drawn silhouette.
One issue is that it is not "cheap" to generate a final image for each sample in each iteration of the MCMC process. Because a piece of the shape is removed and recreated differently in each successive sample, the image can't be reused, so it gets thrown out and regenerated from scratch. If we were only adding to the previous sample, though, we could keep the old image and modify it, which saves valuable computation time.
This is where Sequential Monte Carlo (SMC) sampling becomes useful. SMC sampling was created for making probabilistic inferences as incremental information comes in. In our case, rather than taking a complete shape and mutating it, we can use SMC to guide the search as each rule in the grammar is incrementally broken down into more rules, where samples break down one piece in each iteration of the algorithm. When we calculate score(sample), since the sample is only different from its "parent" due to the addition of one expanded grammar rule, we can instead calculate score_from_parent + score(new piece), where score_from_parent has already been computed from the last round of sampling, so the only new computation is done for the single piece that has been added.
Rather than having one reference shape at a time, SMC holds multiple shapes in each iteration. They all start out as a top-level grammar rule waiting to be broken down. In each sampling iteration, every shape is broken down by one increment. If there were n shapes in this sampling iteration, n shapes are picked to be expanded for the next generation, where shapes with higher scores are more likely to be picked. This means that a very promising partially-generated shape from one iteration can appear multiple times in the next iteration, where each copy continues to be generated independently. This helps the algorithm spend more time exploring the various subtrees of higher-scoring shapes.
This is the algorithm, written out:
- For n samples per iteration, create a fresh top-level grammar rule for each samples[i], 1 ≤ i ≤ n.
- For each samples[i], continue generating its shape by one increment by making one random choice when breaking down grammar rules that are not terminals.
- For each samples[i], calculate likelihood(samples[i]) * score(samples[i]). Call the sum of all of these values total_likelihood_score.
- For 1 ≤ i ≤ n, randomly pick next_samples[i] from samples, where each samples[n] has the probability likelihood(samples[n]) * score(samples[n]) / total_likelihood_score of being picked.
- Set samples[i] = next_samples[i] for each i.
- Return to step 2.
Better score functions
So far, I've just been giving examples for 2D procedural generation. What does a score function look like in 3D? We could still use silhouette matching, but this has some downsides:
- Rendering a 3D scene into a 2D view is expensive, and we have to do it for many samples over the course of one search.
- A silhouette is 2D, so we would only be specifying appearance from one angle, which can be interesting, but isn't super useful.
To address the second point, you can imagine extending the silhouette to 3D. An artist could provide a target 3D shape to fill. This comes with its own concerns:
- Computing 3D space utilization is also fairly expensive. It typically involves voxelizing the model and constructing 3D grids or octrees to record which voxel regions are occupied.
- It's a lot easier to draw a target silhouette than to create a target 3D shape. If you have to model a target shape, it's not that much more effort to just create the final model by hand.
Both of these methods unfortunately still take seconds to run, so artists can't make changes and get realtime feedback.
In an ideal scenario, here's what we would want out of our score function:
- It should be easy for an artist to specify. For example, they shouldn't have to create a detailed 3D model to use the score function.
- It shouldn't overconstrain the search. We want some amount of variation in resulting models, otherwise we wouldn't be using procedural modelling.
- It should work well in 3D.
- The score for a sample should be able to be computed as an addition to the score for the sample's parent so that SOSMC works efficiently.
- It should be computationally inexpensive so that the search can be run at interactive rates.
Model skeletons
Most of the computational inefficiencies in 3D come from dealing with complex geometry. Creating a bitmap image from a model to use in a silhouette comparison involves first applying perspective to every vertex, and then filling in each pixel between these vertices. Matching a target shape in 3D doesn't require perspective to be applied to each vertex, but then instead of filling in pixels, time has to be spent filling in voxels. It is helpful, then, to not look at geometry when making a score function.
Models generated from procedural grammars tend to have some sort of underlying structure in the placement of pieces, regardless of the pieces themselves. In the context of our earlier 2D grammar, I'm talking about the hierarchy produced by saving and restoring paper positions that were made with translate, rotate, and scale. If, every time we change the orientation of the paper, we were to draw a line between the current pen position and the last pen position atop the paper, we would be drawing what looks like the skeleton of the shape. Here is what it looks like in 3D when you do this, connecting points with some diamonds instead of lines:
The nice thing about working with these skeletons is that each "bone" in the skeleton is only defined by two points (or a point and a direction vector.) As long as the final geometry we attach aligns with the hierarchy, we can use a score function that operates on these bones. This isn't a huge assumption, as it takes extra wasted effort for an artist to create a hierarchy and then place geometry that isn't aligned with it. Most models follow this sort of hierarchy, even for models that aren't trees. For example, here is a cathedral, and even with a tangled mess of bones, it is clear that the shapes produced by the geometry and the skeleton are aligned.
Guiding curves
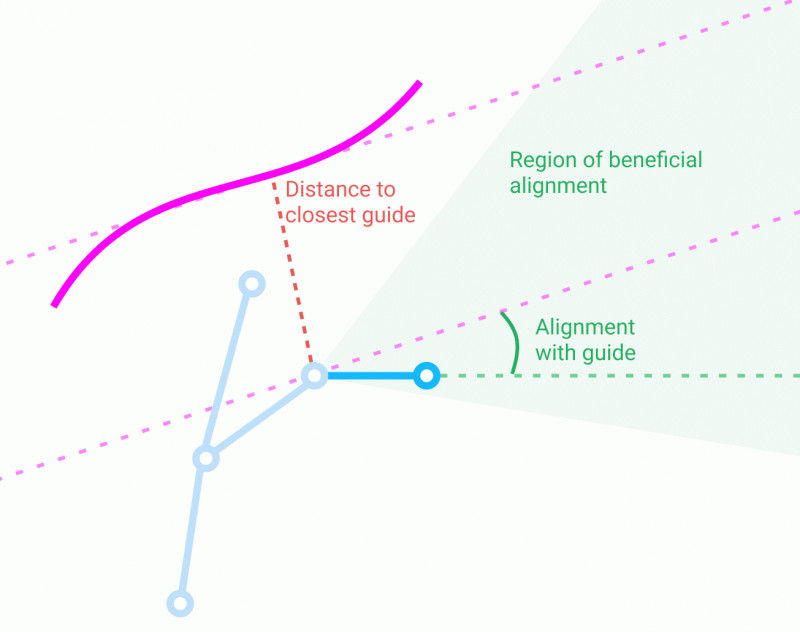
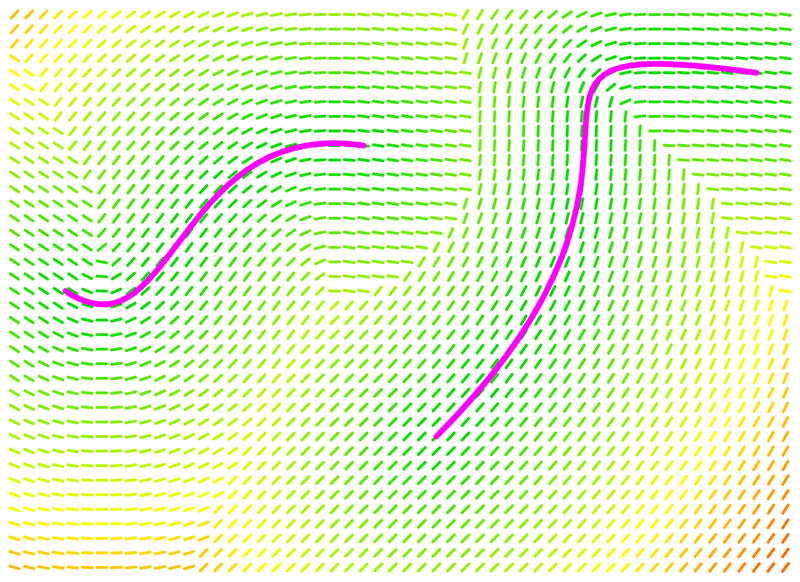
One way to get a score for a model based only off of its skeleton is to compare the bones in the skeleton to guiding curves that an artist draws. For each new bone added when expanding grammar rules, the score is based off of two things:
- Alignment with the guiding curves. The direction of the bone is compared with the direction of the closest guiding curve at the closest point on the curve. Bones that are more precisely aligned get a higher score.
- Distance from the guiding curves. Bones that are closer to a guiding curve get a higher score.
Together, these two factors encourage bones that stick close to the guides and go in the same direction (as opposed to oscillating around the curve.)
But how easy is it to sketch curves in 3D? It turns out, it's not too difficult. When drawing, imagine that, in the center of the 3D scene, there is a glass wall facing the camera. When you draw a new curve, it gets drawn in 3D space as if it were on this glass wall. Edits to the curve similarly operate only on the plane of this wall. To make changes on a different plane, the camera can simply be rotated and repositioned. Here's what that process looks like:
You'll notice that, after drawing or editing a curve, the feedback is pretty immediate. This is something that isn't easily achieved when doing any silhouette or volume matching search.
What can you do with this?
So far I've mostly shown trees built out of simple shapes. This technique starts becoming especially useful once one starts using more complicated models and grammars.
Here are some models created with guiding curves, shown rendered nicely along with the guides used to produce the model. 3D models were imported and used as building blocks that the grammar can then position and drop into the scene. Models generated by the grammar were exported and rendered in Blender.
What's next?
This work is largely a proof-of-concept. While I find it useful for my own tinkering and modelling purposes, experimenting with it has brought to light other parts of the procedural modelling workflow that could use work.
There are enhancements to the guiding curves score function that would be valuable for artists. Applications requiring control of areas and volumes could receive better support. If it can be done while keeping computation time low, it would be useful to give curves finite, specifiable thickness over their lengths. It could provide a more intuitive way to specify regions that uniformly encourage growth. Another extension might include a target density to discourage too many bones from being added in the same region.
While I've spent most of my time talking about ways to efficiently and intuitively search for models created by a grammar, creating the grammar in the first place is still an art requiring a fair amount of skill. When creating a grammar to use with guiding curves, there are still many abstract concepts that you need to keep in your head. Relative coordinate spaces have to be kept in mind when specifying where to place bones, as well as the distribution of bones that will be created when introducing random variation. It would be incredibly useful to spend time thinking about how to make an approachable interface for creating grammars. I would like to be able to define rules visually, seeing the range of space in which bones could potentially spawned, and combine rules with randomization more confidently.
I hope that some of the ideas here can be helpful in producing computer-generated art in new and interesting ways.