Content-Aware Fill for Sequenced Music

Motivation

One of the most socially significant effects the computer era has had on the world is its influence on arts and culture. The next frontier lies in the transformation of the computer from simply being the medium of composition to having an active voice in the composition process, turning it into a dialogue. This work is an incremental step toward that goal by exploring how a computer can assist in the composition process by creating a human-in-the-loop music generation tool.

Goals

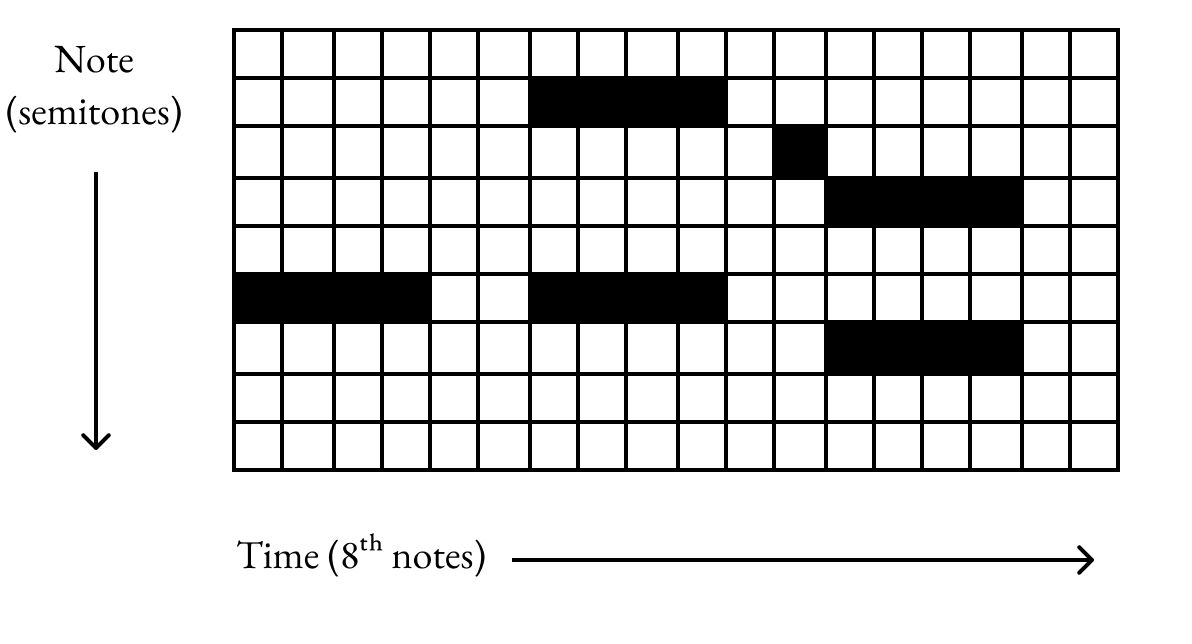
Artists place notes in a piano roll interface when sequencing digital music. After selecting a time range w 8^th notes wide, the computer should fill in the range with notes. The filled notes should have the following properties:

• There should be a smooth transition from the notes preceding the filled region to the filled region and from the filled region to the notes following.
• The notes in the filled region should stylistically match the musical context it inhabits.

Listen

Results are from the more successful model, LSTM+WFC.

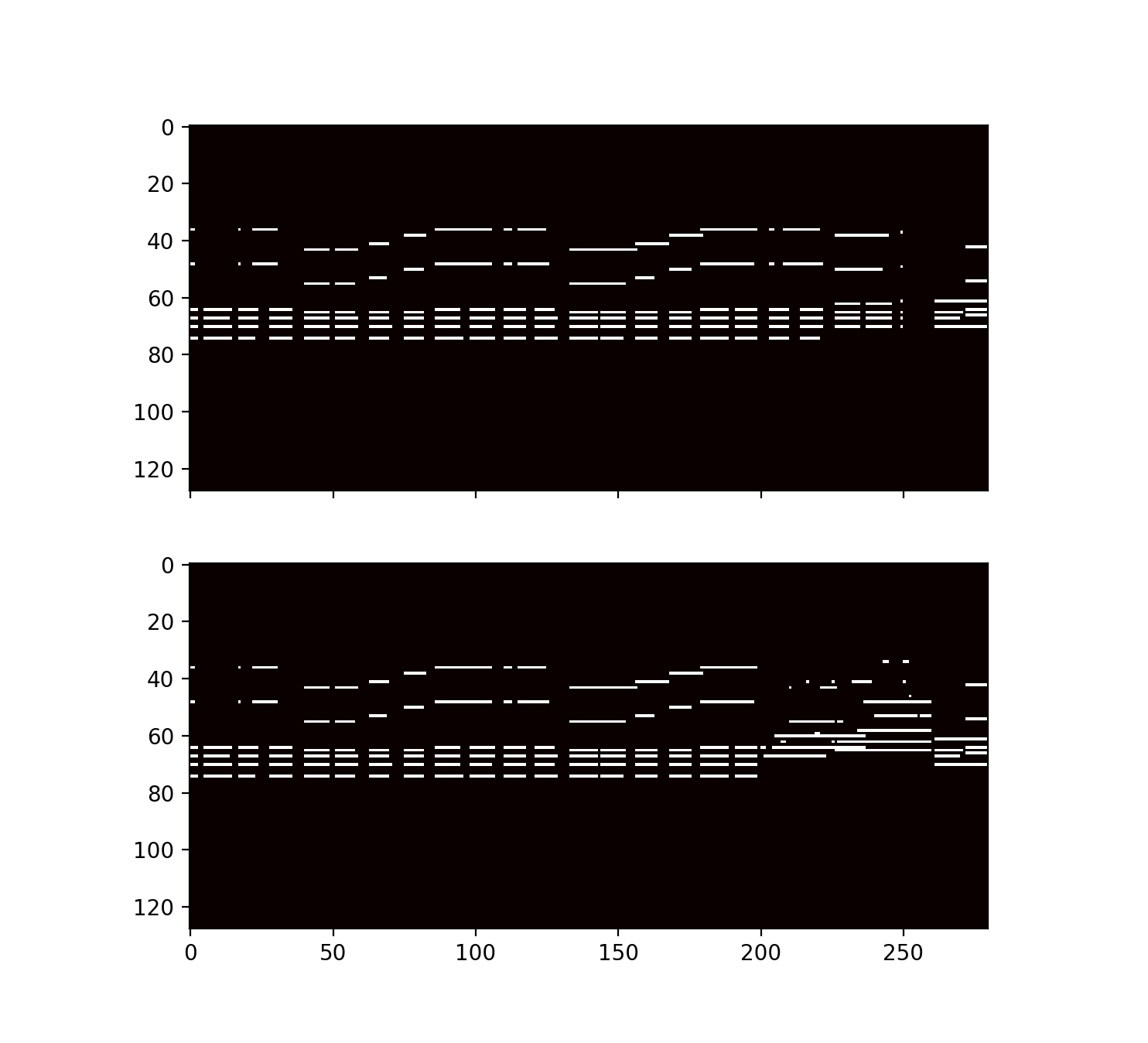	Ground truth
	Filled
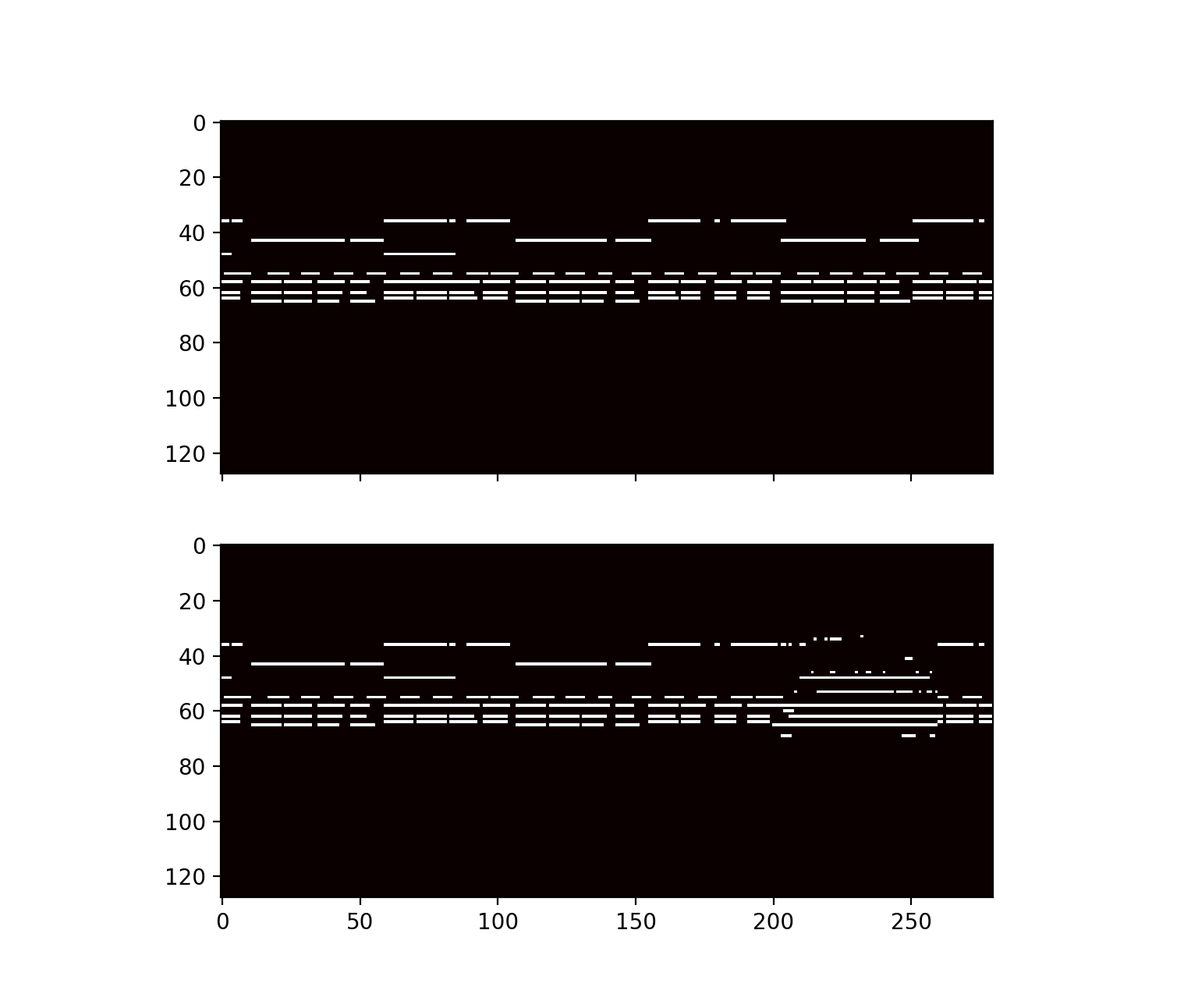	Ground truth
	Filled

Data

Models were trained and evaluated on the piano tracks of the Lakh Pianoroll Dataset, which contains 21,425 multitrack songs. Each piano track is a matrix representing whether note i (where i ∈ [0, 127] is a MIDI pitch with semitone increments) is being sounded at time t (where t is in 8^th notes.)

The objective of the project.

Wave Function Collapse

WFC models divide the input into tiles and create a constraint satisfaction problem when predicting the value of an unknown tile. Two constraints get enforced:

1. Every predicted tile must only be seen adjacent to another tile if the values were seen in the same configuration somewhere in the known region of the grid.
2. The distribution of predicted values should match the distribution of values in the known region of the grid.

Each unknown tile, before it is predicted, is thought of as being the superposition of all possible tile options. A tile option is removed if it has never been seen before in its current configuration with adjacent tiles. When a possible tile is selected, the tile is collapsed to that value, and options for surrounding tiles may become impossible.

While there are remaining tile slots to collapse:

1. Select the tile with lowest Shannon entropy.
2. If it has options, randomly collapse the tile to one of its possible options, where each option has a weight proportional to its distribution in the input notes. Propagate the change to adjacent tiles, update their options.
3. If it has no options, backtrack a random number of choices and try again.

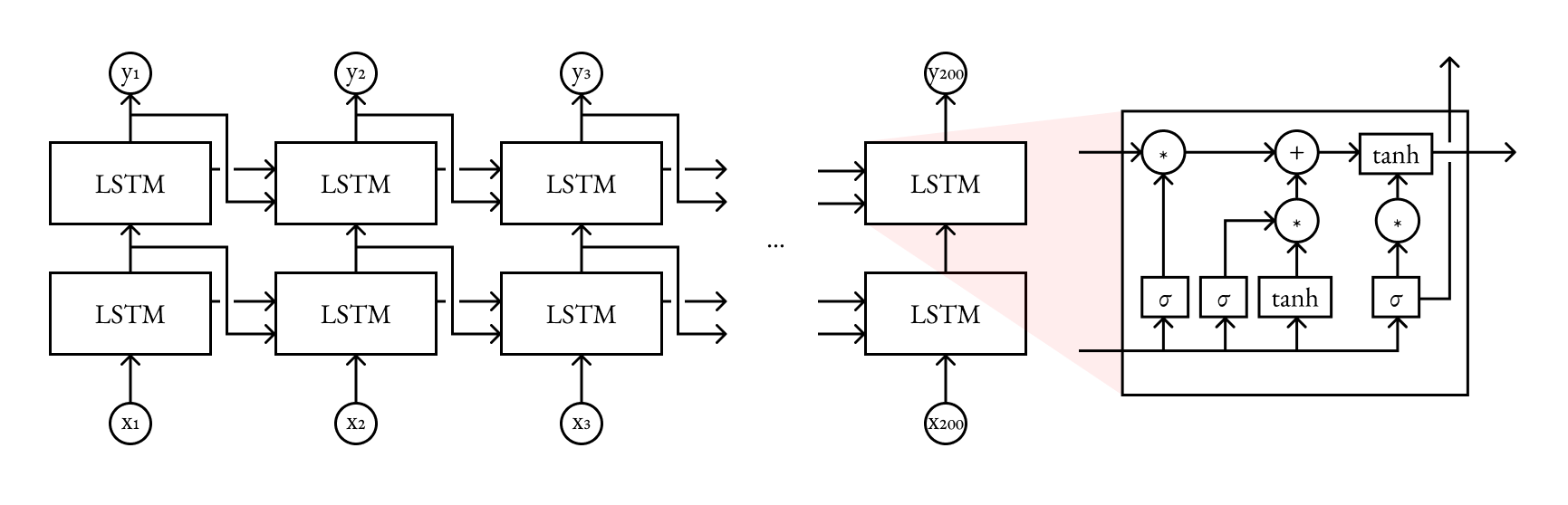
Long Short-Term Memory with Markov Chain Monte Carlo

A trained LSTM network generates notes based on a prefix of 200 notes. This is used to fill a target region. Individual LSTM nodes in the network have a height of 128 since each input and output is a vector holding information for every pitch. Each output y_i represents a vector of probabilities of each pitch being sounded. A boolean vector is sampled for each pitch from these distributions to construct the next time step.

The architecture of the LSTM network.

The LSTM has an output space of possible fillings. The filling that maximizes the likelihood of the suffix s to the filled region is found using Markov Chain Monte Carlo sampling:

1. Initialize f₀ by generating a filled region
2. For i = 0 to N:
   1. Sample u ~ U(0, 1).
   2. Sample n ~ U{1, w}.
   3. Sample f_* by rewinding f_i-1 by n 8^th notes and regenerating n new 8^th notes.
   4. If u < (P(s|f_*)P(f_*)) / (P(s|f_i-1)P(f_i-1)), set f_i = f_*.
   5. Otherwise, set f_i = f_i-1.

Results

A piano roll can be thought of as a Markov chain, where the notes being sounded at time t are a state of a Markov process. The transitions between states have probabilities corresponding to how often those two states occur next to each other. States can use pitch number mod 12 to be invariant to the octave of the pitch.

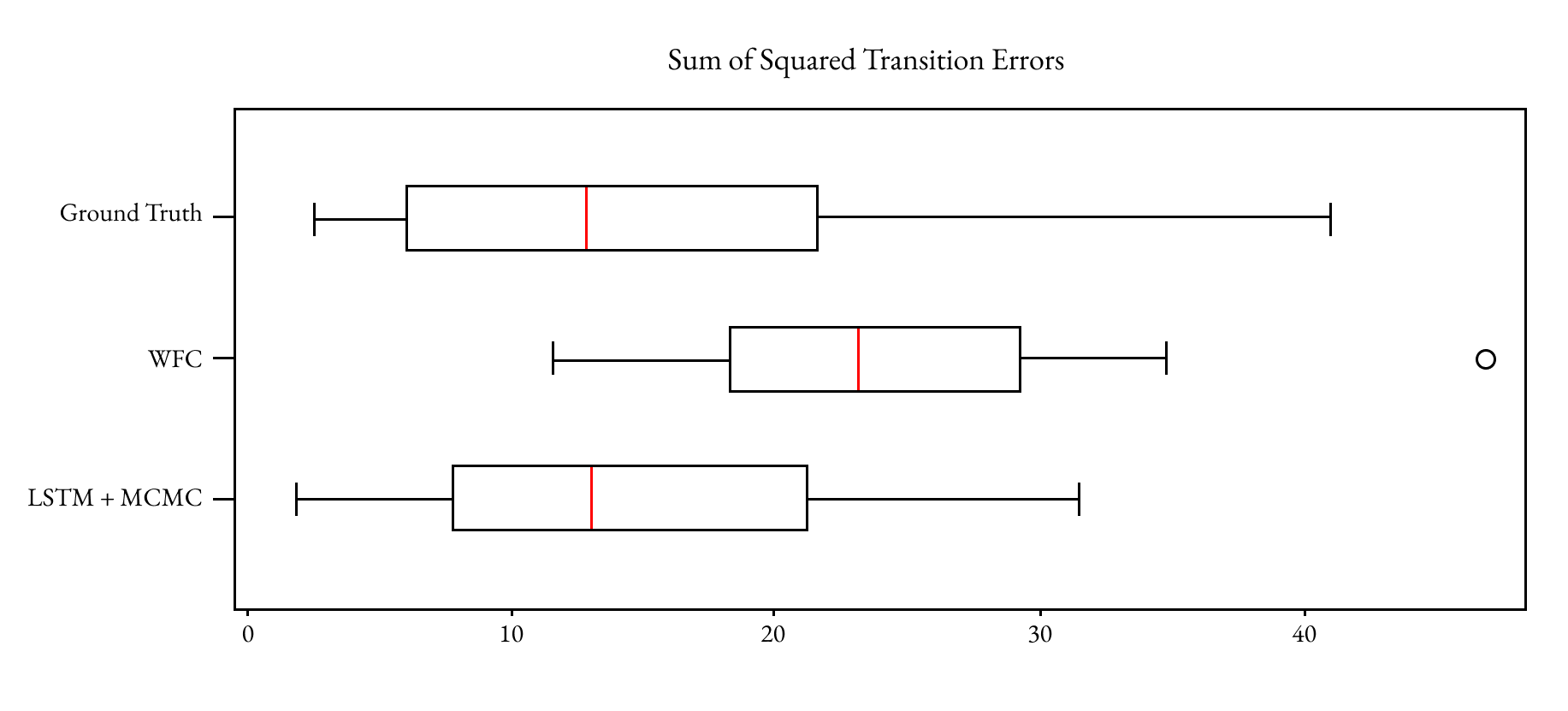
The piano roll from the filled region is modelled as one Markov process and the rest of the piano roll is modelled as another. Assuming piano rolls can be thought of as both being products of the same Markov process, the difference between two processes can be used as a proxy for stylistic fit. Markov process transition probabilities from the filled regions in the ground truth, from WFC, and from LSTM+MCMC were compared against the transition probabilities from the Markov process for the surrounding notes.

Errors in the Markov process state transition matrices between various sources and the unfilled region of the song.

• The LSTM+MCMC model produces a similar median error to the ground truth.
• Neither reaches zero due to noise from the filled region not having many samples.
• Both learned models have less variance than the ground truth: real human composers are not perfect Markov processes and can produce "surprising" scores.
• Both have issues continuing obvious structured, repeating patterns.