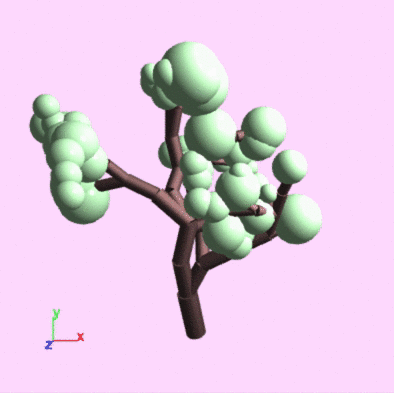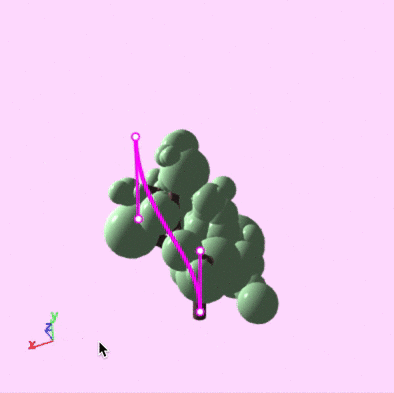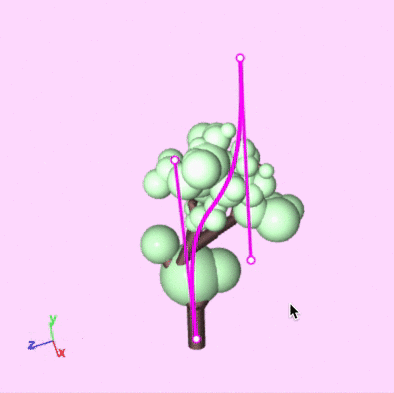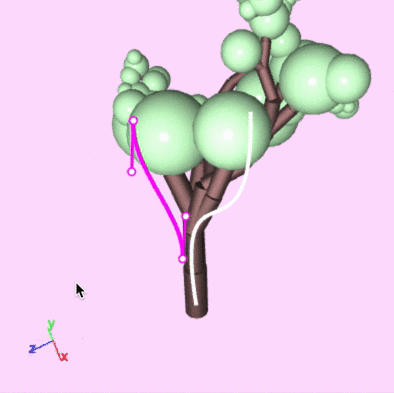
Controlling procedural modelling interactively with guiding curves

Proceedings of Graphics Interface

We present a likelihood function for Sequential Monte Carlo sampling that lets artists draw guiding curves to control the output of generating grammars. This framework enables the high-level structure of models to be intuitively specified while allowing for sufficient variation in the low-level details. Our method can be computed at interactive rates to enable the short feedback loops required for exploratory design.

We additionally created a proof-of-concept editor that uses this method to enable real-time searching of models produced by a grammar to demonstrate this capability.

The guiding curves editor, with a pane on the left to create a generating grammar, and a pane on the right to draw guiding curves.

Why interactive procedural modelling?

Procedural modelling is a great way to add a level of detail and richness to 3D modelling that would be impractical to create by hand. It is used, for example, to apply patterns to large scales to create whole landscapes, or on a smaller scale to create varied individual plants and creatures.

Grammars are a convenient way to express those patterns. Unfortunately, they produce a broader space of models than would be artistically desirable. For each good model produced, there may also be a weird one. Editing the grammar to prevent this is extremely hard (consider trying to modify the English grammar to prevent gross sentences from being valid for a sense of how hard this can be.)

An alternative is to search the space of models produced by a grammar for samples that best fit a set of constraints. You can think of the constraint search as controlling the growth of generative models. Past work has used probabilistic inference to do the search and has provided constraints on properties such as the volume a model occupies and the shape of its shadow. However, it takes a lot of effort to create targets for these constraints, and they take tens of seconds to run a search on. This prevents artists from working iteratively, where there is a quick feedback loop between the artist and the tool. Ideally, we would have a workflow where the artist makes changes, looks at interactive feedback, and uses that to make more changes. This sort of feedback requires the search to run in under a second. This work aims to do as much useful work for the artist as possible in under a second to enable iterative design.

Drawing guiding curves

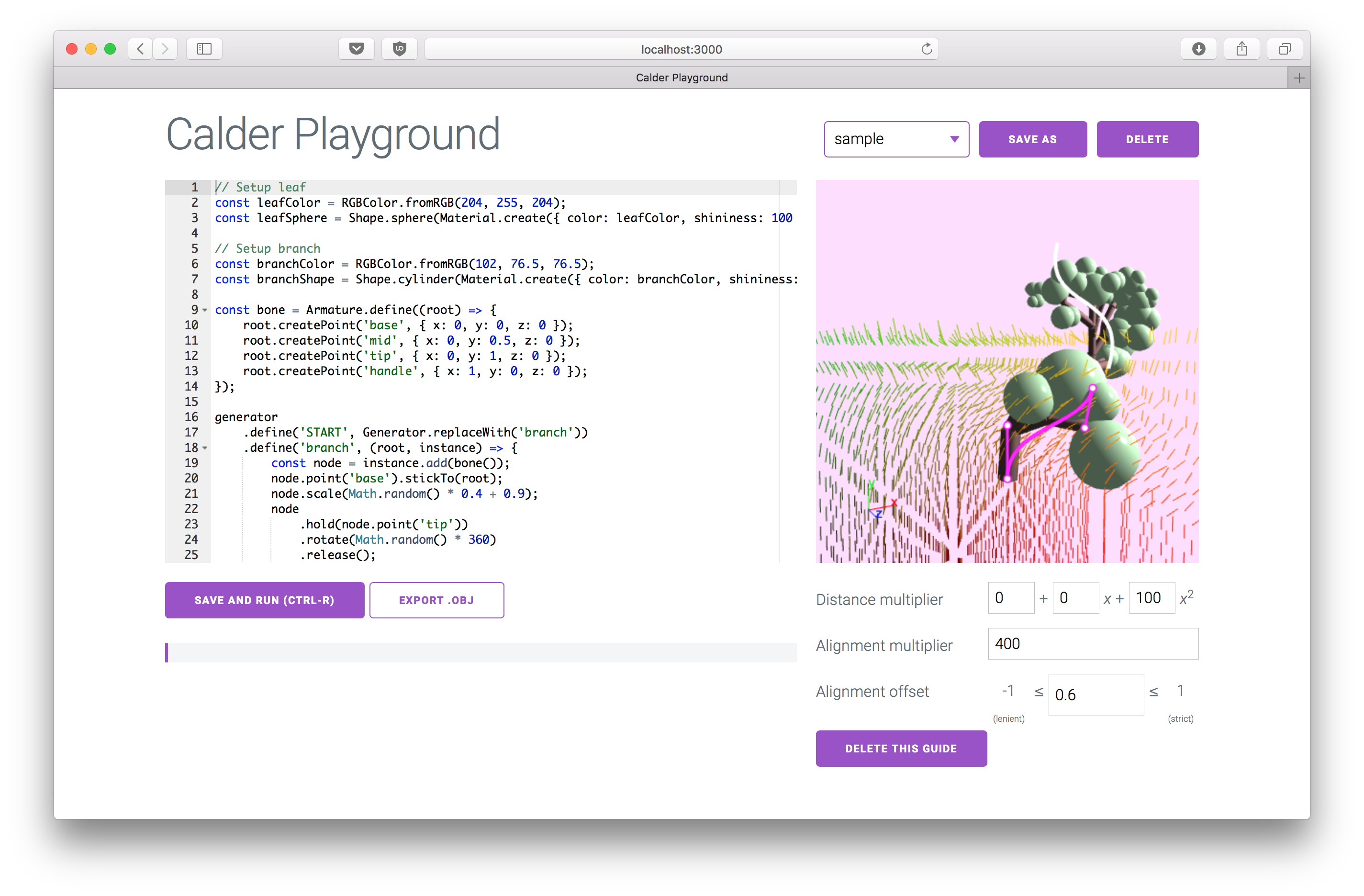
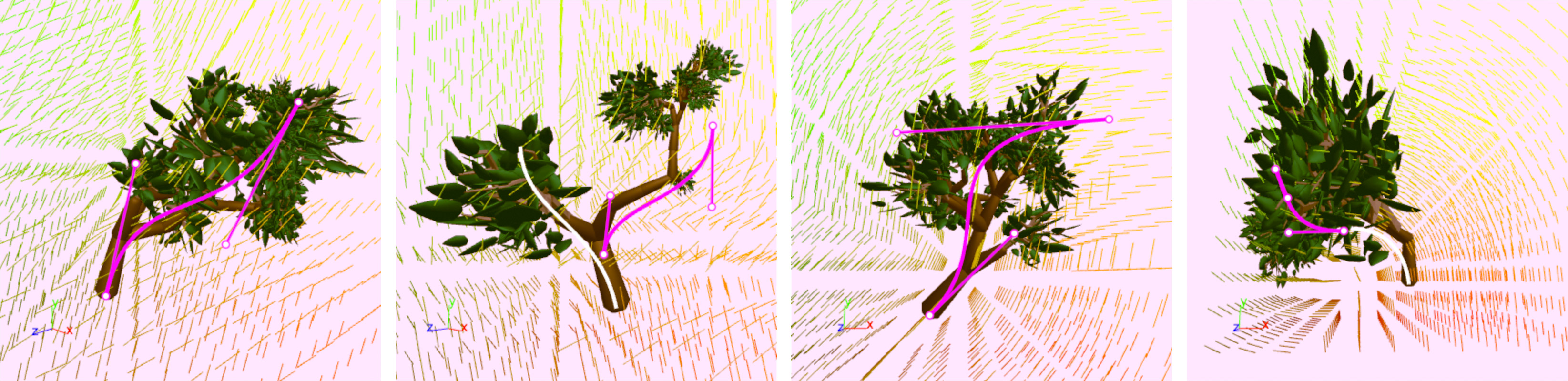
We created an editor that lets you write a grammar and then explore the space of models generated by the grammar by drawing guiding curves.

A demonstration of drawing and editing guiding curves and getting real-time feedback.

When we generate a model, we start by just constructing a skeleton of the model. Curves are used to assign a cost to "bones" of the skeleton, and we run optimization to find a skeleton with the lowest total cost. We then turn the skeleton into an actual model by adding final geometry to the bones.

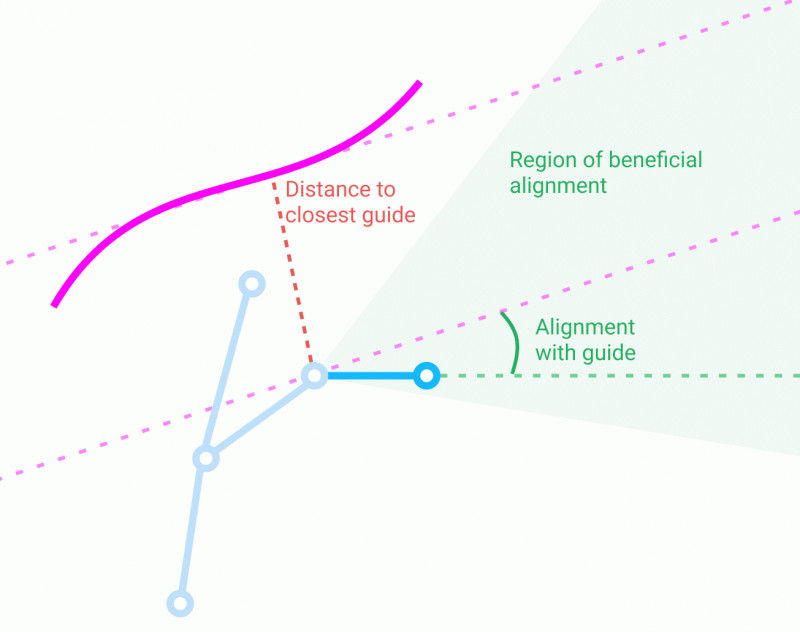
For each bone, there are two factors affecting the cost:

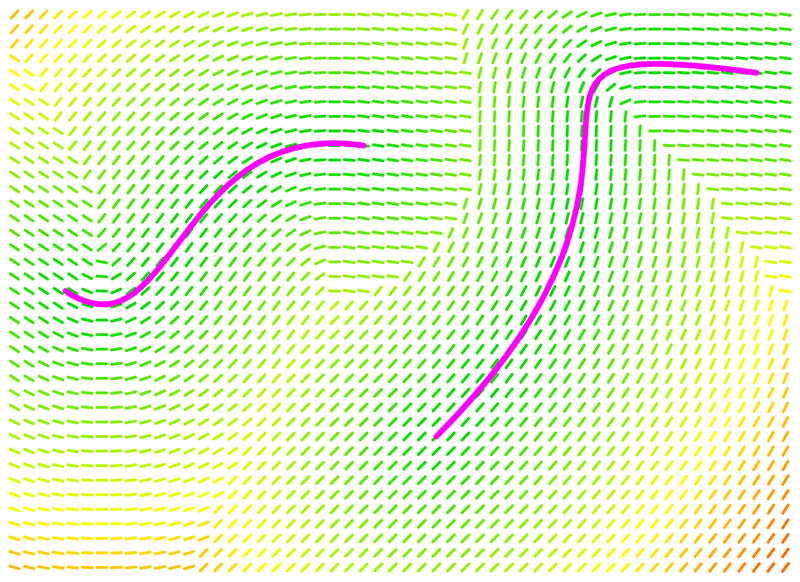
1. Alignment to a vector field. We find the closest point on a guiding curve to the base of the bone and see how closely the direction of the bone aligns with the gradient of the curve at the closest point. Well-aligned bones have a negative cost, incentivizing adding well-aligned bones; poorly-aligned bones have a positive cost. How well-aligned a bone needs to be to have a negative cost is a tunable parameter.

2. Distance to the guiding curve. When we find the closest guiding curve, we add a cost based on how far away the bone is to balance the alignment cost. You can pick if you want the cost to scale linearly or quadratically with distance.

The information the cost function operates on when adding a new bone.

The alignments for each point in space around some guides, coloured to represent the distance cost for that location.

Examples

A procedural tree.

A procedural cathedral.

An abstract, modular treehouse.

Procedural abstract art inspired by the work of Mondrian. Subdivision happens at successively large *y* values, so guiding curves reach into space to specify regions of higher subdivision.